Moule conique modulable pour gâteaux à la broche

Le gâteau à la broche est une spécialité très populaire dans les Hautes-Pyrénées. La recette traditionnelle comporte essentiellement de la farine, du beurre, du sucre et des œufs. A cela on rajoute des aromates selon les goûts de chacun. Personnellement pour moi, arôme naturel de vanille, rhum et poudre d’amandes.
Pour la proportion des ingrédients : On choisit 1 kg de farine, 1 kg de beurre et 1 kg de sucre pour 2 douzaines d’œufs.
Le moules est constitué de plusieurs éléments :
1°) Un cône qui peut comporter une bague en aluminium ou un insert permettant de le fixer sur la broche à l’aide d’une vis de 6 mm six pans creux. On l’appellera : « cône primaire ».
2°) une série de modules (en forme de tronc de cône) qui viennent se juxtaposer en fonction de la taille du gâteau que l’on souhaite réaliser.
3°) Une bague de serrage venant à l’arrière du dernier élément emboîté pour maintenir l’ensemble.
Le moule a été conçu pour réaliser des gâteaux en utilisant pour la recette : 6 œufs, 8 œufs, 10 œufs, 12 œufs, 15 œufs, 18 œufs, 21 œufs ou 24 œufs avec une épaisseur moyenne de 2,5 cm pour le gâteau.
Le premier cône utilisé seul permet de faire un gâteau avec 6 œufs. Un premier élément rajouté permet de faire un gâteau avec 8 œufs. Un deuxième élément rajouté permet de faire un gâteau avec 10 œufs….. et ainsi de suite. On va ainsi utiliser 8 tailles différentes correspondant chacune à 6, 8, 10, 12, 15, 18, 21 et 24 œufs pour la recette.
Le cône primaire aura la taille T6 correspondant à 6 œufs.
Les éléments suivant auront respectivement les tailles : T8, T10, T12, T15, T18, T21 et T24
Comment définir la dimension de chaque élément ?
Tout d’abord, il faut définir la conicité. Un angle de 7° a été choisi entre une génératrice du cône et l’axe de la broche. Ce qui donne une conicité de 24,5% (24,5569% plus précisément). Une telle conicité permet un démoulage facile après la cuisson et donne au gâteau un profil des plus harmonieux.
Ensuite, il a fallut faire une évaluation du volume de gâteau obtenu pour une quantité d’ingrédients donnée. En l’occurrence, 3000 cm3 pour une recette avec 24 œufs. Cette valeur s’est ensuite révélée très exacte pour obtenir une épaisseur de gâteau de 2,5 cm en moyenne. Cela représente donc 125 cm3 de gâteau pour 1 œuf.
Calculs:
Les calculs vont faire appel à 3 notions fondamentales qui sont :
1°) La conicité
2°) Le volume d’un tronc de cône.
3°) La résolution d’une équation du second degré.
(mathématiques niveau « seconde » du lycée)
Mais même si les maths sont pour vous un casse-tête, ce n’est pas grave car je vais vous donner toute la solution. Il suffit de suivre les dimensions indiquées dans le tableau ci-dessous.
1°) La conicité :
Nous l’avons déjà vu plus haut. Elle est de 24,5% (soit 0,24557) pour un angle de 7°
La formule : C = 2 tan (α)
Ou bien : C = (D-h)/H
(Différence entre la base et le sommet….le tout divisé par la hauteur)
2°) Le volume d’un tronc de cône :
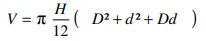
Avec :
V volume du tronc de cône
H Hauteur du tronc de cône
D Diamètre de la base
d Diamètre du sommet
π égal à 3,14
3°) Calcul de la hauteur:

Soit :
d1 Le diamètre au sommet du moule
D1 Le diamètre à la base du moule
d2 Le diamètre au sommet du gâteau
D2 Le diamètre à la base du gâteau
C La conicité
H La hauteur
V Le volume du gâteau une fois démoulé
V1 Le volume du moule (a, b, c, d)
V2 Le volume du gâteau avec celui du moule (e, f, g, h)
Avec : V = V2 – V1
De la formule de la conicité, on déduit: D = d + CH ( soit : D1 = d1 + CH et D2 = d2 + CH )

De la même manière, on peut calculer:

On a défini : v=125 cm3 pour 1 œuf
Si T est la taille du cône ; on aura alors : V = 125 T
Et on peut établir la hauteur du cône en fonction de sa taille :
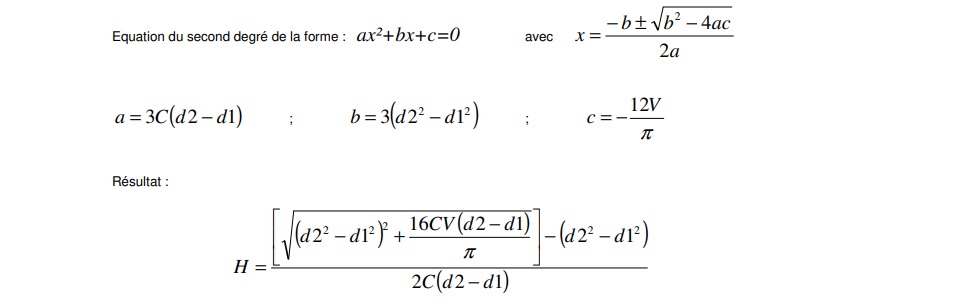
Connaissant :
La conicité « C »: 0,24557
Le diamètre au sommet du moule « d1 » : 2,2 cm
Le diamètre au sommet du gâteau « d2 » : 7,1 cm (soit d1 + 2 fois l’épaisseur du gâteau)
Epaisseur du gâteau : 2,45 cm environ
La relation précédente simplifiée devient :

On peut ainsi calculer la hauteur pour chacune des tailles T6, T8, T10, T12, T15, T18, T21 et T24 et en déduire la hauteur de chaque élément.
On peut ensuite connaître le diamètre au sommet et à la base de chaque élément en utilisant la formule : D=d+CH.
Les calculs sont regroupés dans le tableau et dans le dessin suivant :

On peut constater que la hauteur de chaque élément diminue au fur et à mesure de l’empilement des modules. Ce qui est logique dans la mesure ou le diamètre augmente à chaque empilement et dans la mesure ou le volume du gâteau augmente de la même quantité (d’une façon linéaire) d’une taille à la suivante. La diminution en hauteur des éléments se fait suivant une courbe parabolique caractéristique de la fonction du second degré établi dans les calculs
.Maintenant que l’on connaît la dimension des différents éléments, on peut entreprendre la fabrication. Les éléments ont été taillés dans un bois dur et réalisés au tour (tour à métaux car je n’ai pas de tour à bois). Beaucoup d’essences conviennent (Hêtre, frêne, Houx, chêne, merisier, arbres fruitiers….). J’ai utilisé le bois que j’avais sous la main. Le moule montré sur la photo en première page a été réalisé en frêne, merisier et chêne.
C
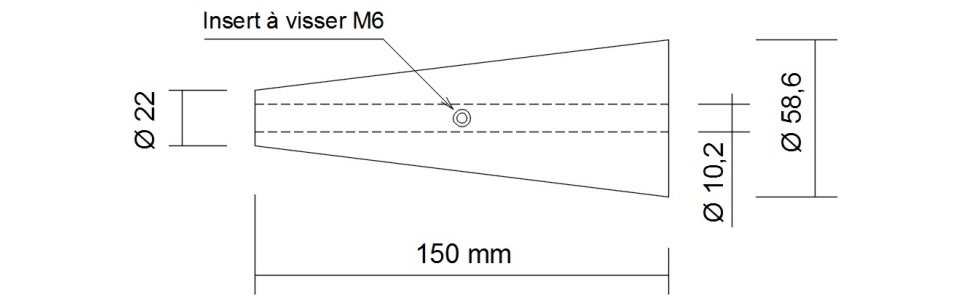
Cône secondaire T8 (représentation en coupe):
Le retrait au centre de 1 mm pratiqué côté du plus petit diamètre permet une meilleure assise et un meilleur serrage des éléments les uns contre les autres.
Les autres modules : T10, T12, T15 T18 T21 et T24 suivent le même plan en respectant leurs dimensions respectives en ce qui concerne le petit diamètre, le grand diamètre et la hauteur suivant le tableau des dimensions ci-dessus.
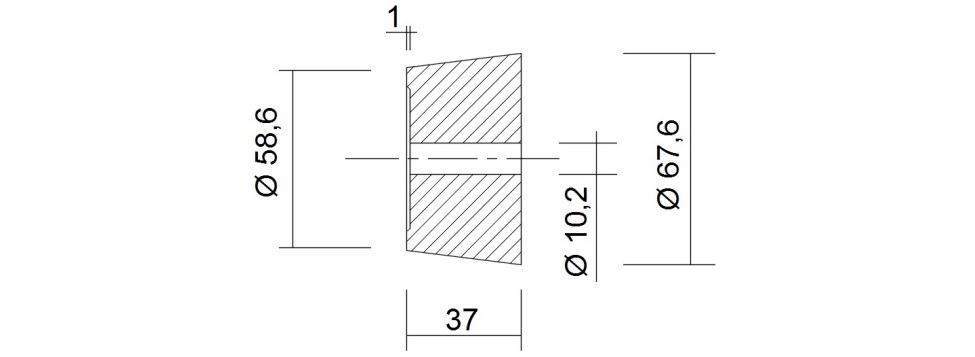
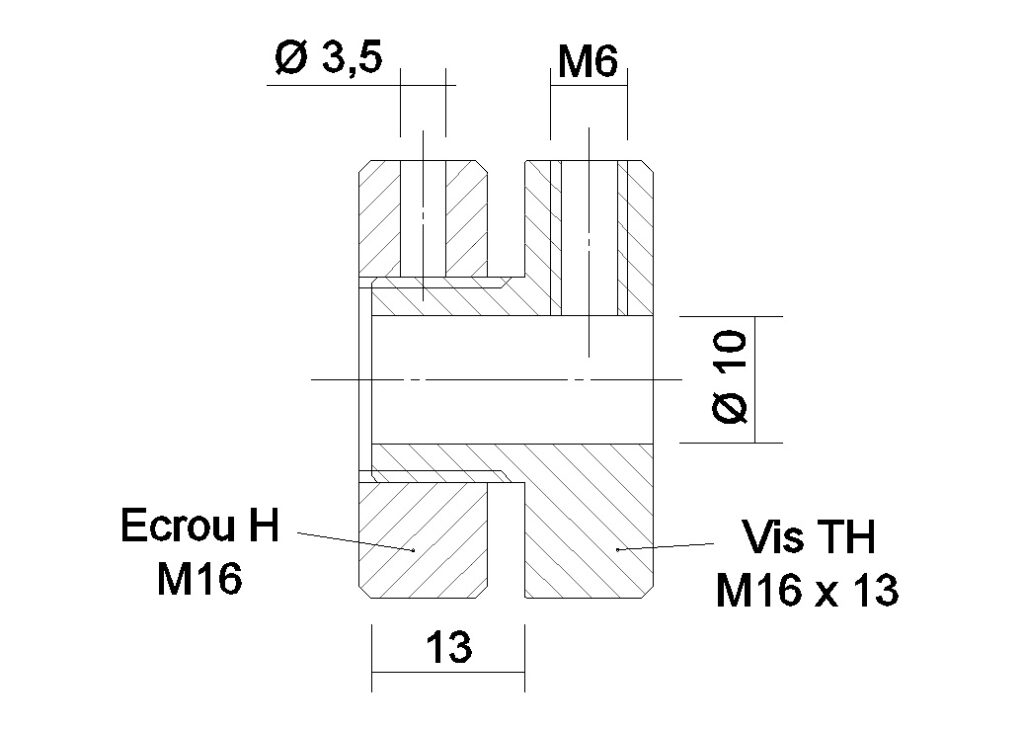
Douille de serrage ou de maintien (représentation en coupe):
Cette douille est constituée d’une vis à tête hexagonale M16 d’une longueur de 13 mm percée en son centre au diamètre 10 pour pouvoir s’enfiler sur la broche du moule. Un trou taraudé M6 est pratiqué sur l’une des faces de la tête de vis. Il reçoit une vis de pression 6 pans creux (longueur 10 à 12 mm) permettant un blocage sur la broche.
L’écrou H M16 permet de serrer les modules les uns contre les autres pour assurer une rigidité et une cohésion de l’ensemble. Cet écrou est percé d’un trou de diamètre 3,5 mm pour permettre sa rotation et le serrage par l’intermédiaire de la clé allen de 3 utilisée pour la fixation du cône primaire et le blocage de la douille sur la broche.

Entraînement de la broche en rotation:
Au delà d’entraîner la broche à la main avec une manivelle, il est préférable d’utiliser un moteur. Pour ma part, j’ai utilisé un moteur 12V d’essui glace de voiture en réalisant moi-même une régulation de vitesse PWM à l’aide d’un circuit intégré NE555.
Sinon, on peut trouver (sur internet) des motoréducteurs à courant continu et régulateurs de vitesse qui conviennent parfaitement pour réaliser cet entraînement. J’indique ci-dessous le type de produit qui peuvent convenir. L’idéal est de faire tourner le moteur à une vitesse d’environ 40 tours/mn à partir du début de la cuisson, puis d’augmenter la vitesse jusqu’à environ 90 tours à 100 tours/mn en fin de cuisson pour réaliser des pics sur le gâteau. On trouve sur internet des motoréducteurs tournant à la vitesse de 130 tours/mn et je pense que ces moteurs peuvent parfaitement convenir. L’alimentation 12V peut aussi être obtenue par l’utilisation d’une simple batterie 12V. On peut également certainement trouver des contrôleurs de vitesse en boîtier plastique ou métal.
J’ai eu l’occasion d’utiliser ce type de moteur (en 40 tours/mn) avec ajout d’un étage supplémentaire de réduction pour soulever un poids de 10 kg. Ce qui indique que ce type de moteur possède la puissance suffisante pour faire tourner le moule d’un gâteau à la broche.


moteur à courant continu
(moins de 10€)

(15€ à 20€)

